
When evaluating or improving the performance of an LLM application, we often focus first on the model itself and then on crafting the prompt to get the best possible results. There’s no shortage of resources on best practices for prompt engineering. In contrast, detailed explanation and guidance on how to set the temperature parameter is harder to come by. This article aims to close that gap.
While this article includes a few mathematical formulas for readers who want to understand the details, you don’t need a math background to follow along. Each concept is explained intuitively, allowing you to grasp the ideas without needing to work through the equations.
How do LLMs generate text?
LLMs generate text by iteratively predicting one token at a time. At each step, the model analyzes all previous tokens, including those it has already generated, to produce a probability distribution over possible next tokens. It then samples from this distribution to select the next token, repeating this process until it reaches an end-of-sequence token.
Example
- User: Answer with exactly two words. What is the meaning of life?
- Assistant: Love others.
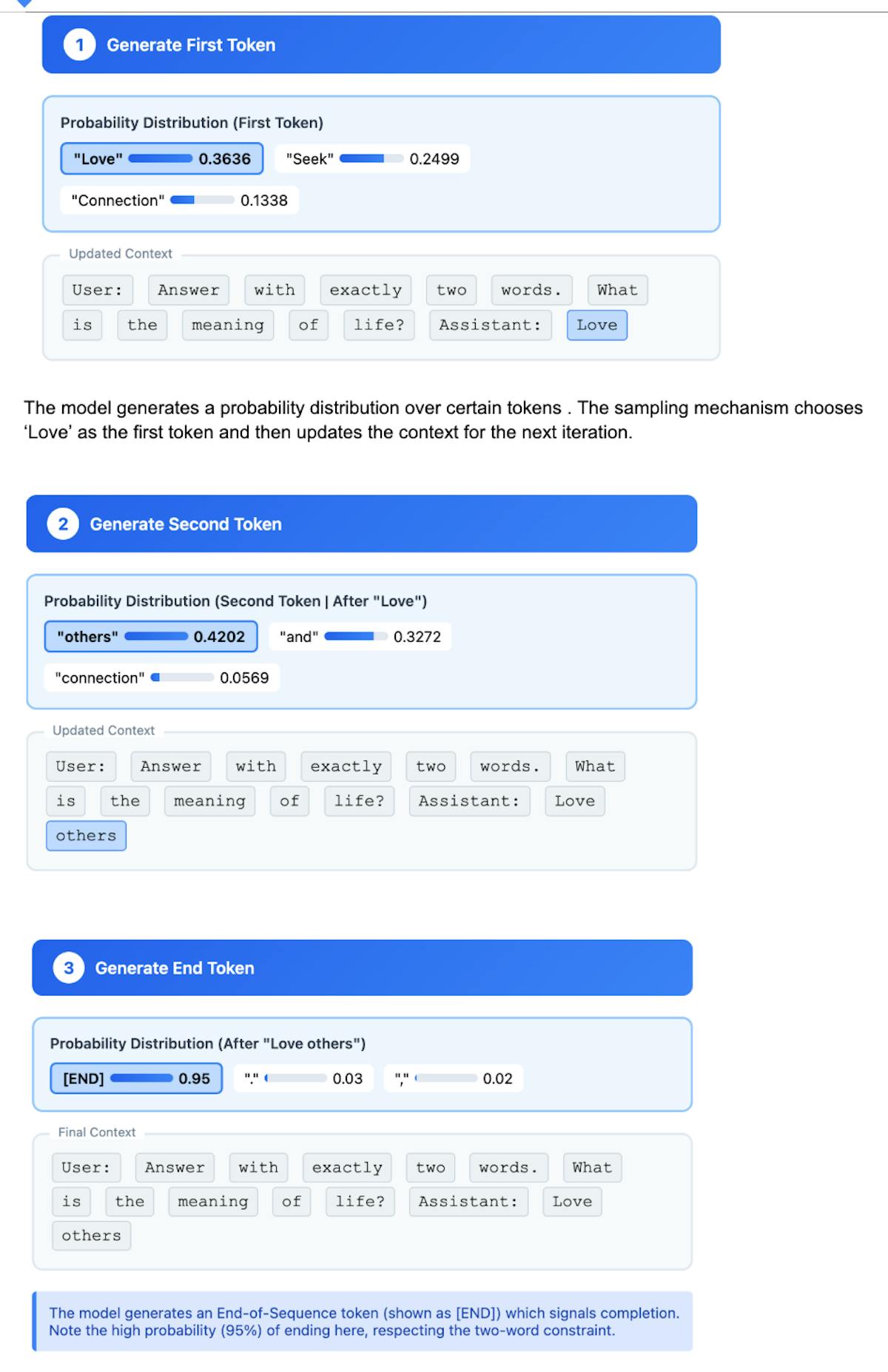
This example is based on actual token probabilities observed for the gpt4o-mini model in early August 2025.
Sampling from a Probability Distribution
Let’s examine what sampling from a probability distribution looks like for an LLM. Each LLM inference step (over all those billions of parameters) produces a probability distribution for a ‘next token’.
P(xₜ₊₁ | x₁:ₜ) = LLM₍θ₎(x₁:ₜ)
Where,
Input: x₁:ₜ — sequence of tokens so far
Output: P(·) — probability distribution over the vocabulary for the next token.
More explicitly, P(·) is a vector of probabilities, one value for each token in the vocabulary.
Each value represents how likely the model thinks that token will be the next token, given the sequence so far. All probabilities are between 0 and 1, and sum to exactly 1.
θ: model parameters (weights of the LLM)
What does it mean to sample from a distribution?
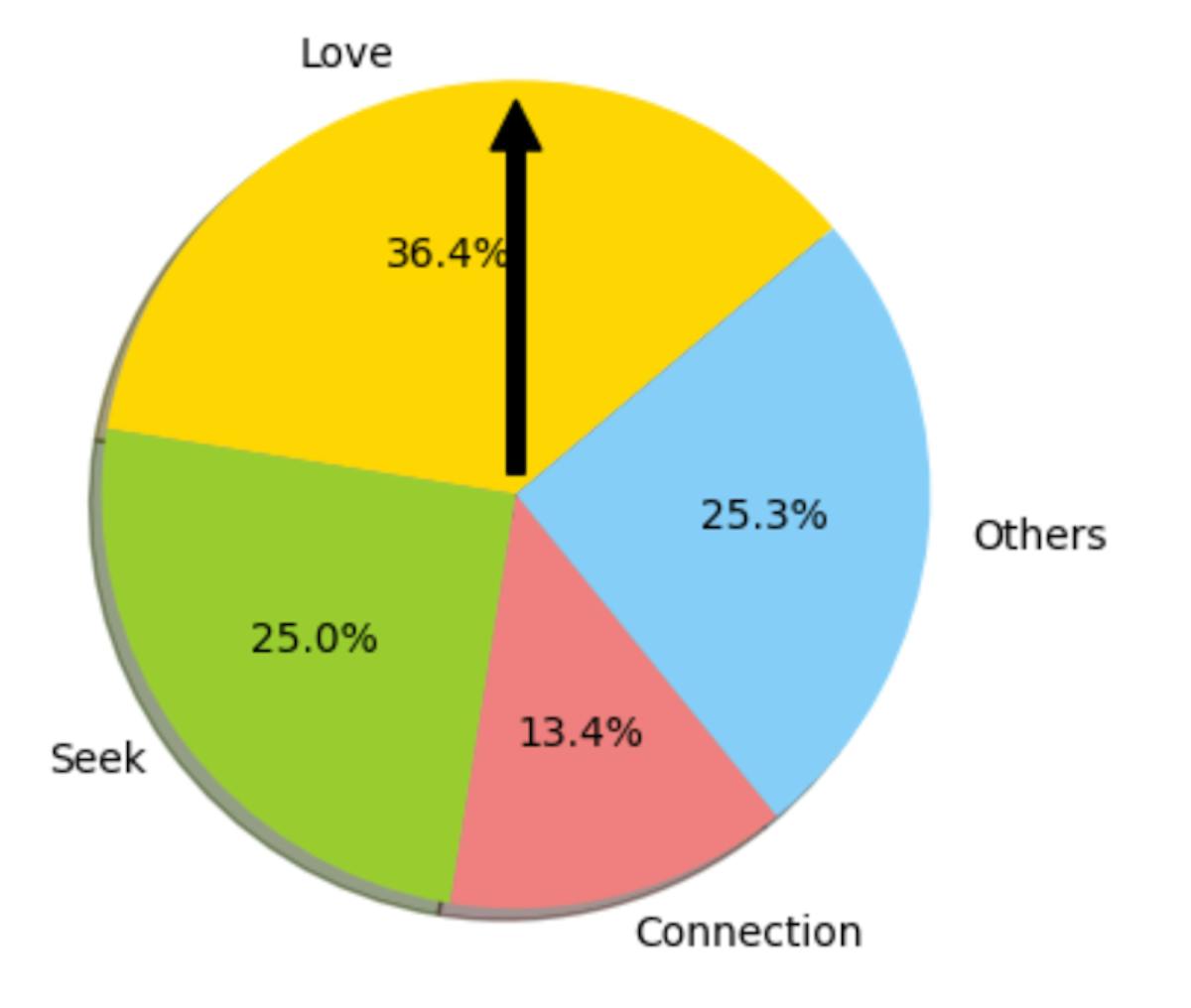
Suppose your probability distribution for the next token is this
- P(Love) = 36.4%
- P(Seek) = 25.0%
- P(Connection) = 13.4%
- P(Other tokens) = 25.3%
Imagine spinning a wheel of fortune to pick the next token—the pointer lands on one slice, and that’s the token the model outputs. The size of each slice represents that token’s probability of being chosen next.
A natural question is: why don’t we always choose the most likely token? The reason is that this leads to boring, repetitive text. While that may be acceptable for domains with a single correct answer, it is not ideal for creative outputs.
So, why not simply sample from the model’s probability distribution, as in the “wheel of fortune” example above? Over a long sequence of output tokens, the sampling mechanism is likely to select a low-probability token at some point in generation. This can cause the model’s output to drift in an undesirable direction.
What we need is a mechanism that allows us to choose an intermediate point between these two extremes—and this is where the temperature setting comes in.
A temperature of 0 puts all the weight on the highest-probability token. A temperature of 1 preserves the original distribution. Higher values, such as 10 or above, give roughly equal weight to all tokens, making the model’s output likely unhinged and potentially nonsensical—which is why OpenAI caps the temperature at 2.
Now let’s dive deeper into the math behind the scenes. It is helpful to understand this, even at a high level to get some intuition about the temperature setting.
The Softmax Function
The softmax function is used to normalize a vector of numbers over any range so that their values lie between 0 and 1 and sum to 1, allowing them to be interpreted as probabilities.
The probability distribution of a model is obtained by applying the softmax function to the raw, unnormalized scores (called logits) that a language model outputs for each token in its vocabulary.
If the model produces logits (a1,a2,…,an), then the softmax probability distribution is given by:
pᵢ = exp(aᵢ) / Σⱼ exp(aⱼ) for j = 1..n (Equation 1)
This converts raw logits a₁, a₂, …, aₙ to probabilities p₁, p₂, …, p
Bounded probabilities:
0 ≤ pᵢ ≤ 1
since exp(aᵢ) > 0 and the denominator is the sum of positive terms.
Sum to one:
Σᵢ pᵢ = 1 for i = 1…n (Equation 2)
because the sum of the numerators equals the shared denominator.
log probability is defined as:
zᵢ = ln(pᵢ) (Equation 3)
It can be shown that:
aᵢ = zᵢ + C
where C is a constant that can be added to all zᵢ without changing the resulting pᵢ.
From here, we work directly with log probabilities (Zi) because they simplify calculations and are also what the OpenAI API returns if requested.
pᵢ = exp(zᵢ) / Σⱼ exp(zⱼ) for j = 1…n (Equation 4)
Note that:
- exp(zᵢ) = exp(ln(pᵢ)) = pᵢ by the definition of ln,
- The denominator is simply 1 (by Equation 2), this equality holds directly.
The Scaled Softmax
We now want our softmax to be more flexible—i.e., to have a way to adjust the model’s probability distribution in our desired direction.
The scaled softmax is defined as:
pᵢ(T) = exp(zᵢ / T) / Σⱼ exp(zⱼ / T) (Equation 5)
Here, we have simply divided the log probability zᵢ by T in the definition of pᵢ.
How does this help?
A useful way to understand the behavior of this equation (and many others) is to examine its extreme values and some special cases.
As T → 0 when T becomes arbitrarily small, the denominator is dominated by the largest value of zᵢ.This is because scaling replaces exp(zᵢ) with exp(zᵢ/T). By basic algebra:
exp(zᵢ / T) = (exp( 1 / T) ) ^ zⱼ
When T is very small, 1/T becomes very large, so the highest zᵢ term dominates the sum in the denominator for equation 5. Consequently, the probability of selecting the most likely token approaches 1.0.
T=1: We recover the original model probability distribution. Equation 5 reduces to Equation 4 in this case.
As T → ♾️, all exp(zi/T) become exp(0) and hence, the probability of each token becomes equal. You don’t need a language model for this! It will essentially just produce random sequences. In fact as T increases beyond 1 (See references) the model output quality drops significantly.
Most of the useful values of T lie between 0 and 1, corresponding to probability distributions that range between always choosing the most likely token and sampling according to the model’s original probability distribution.
The Effect of Different Temperature Settings
Let’s examine what happens to the probability distribution as we vary the temperature.
| Token | Model Probability | Logprob | Sampling Probability at T = 0 | T = 0.5 | T = 1 | T = 2 | T → ♾️ |
| Love | 0.3636 | -1.0117 | 1.0 | 0.4783 | 0.3636 | 0.3059 | 0.25 |
| Seek | 0.2499 | -1.3867 | 0.0 | 0.2259 | 0.2499 | 0.2536 | 0.25 |
| Connection | 0.1338 | -2.0114 | 0.0 | 0.0648 | 0.1338 | 0.1855 | 0.25 |
| Other Tokens | 0.2527 | -1.3756 | 0.0 | 0.2310 | 0.2527 | 0.2550 | 0.25 |
Note: ‘Other Tokens ’is not a single token (we created a compound token with all the tail tokens so that the sum of probabilities is 1)
Visually examining the sampling Distributions for Different Values of T
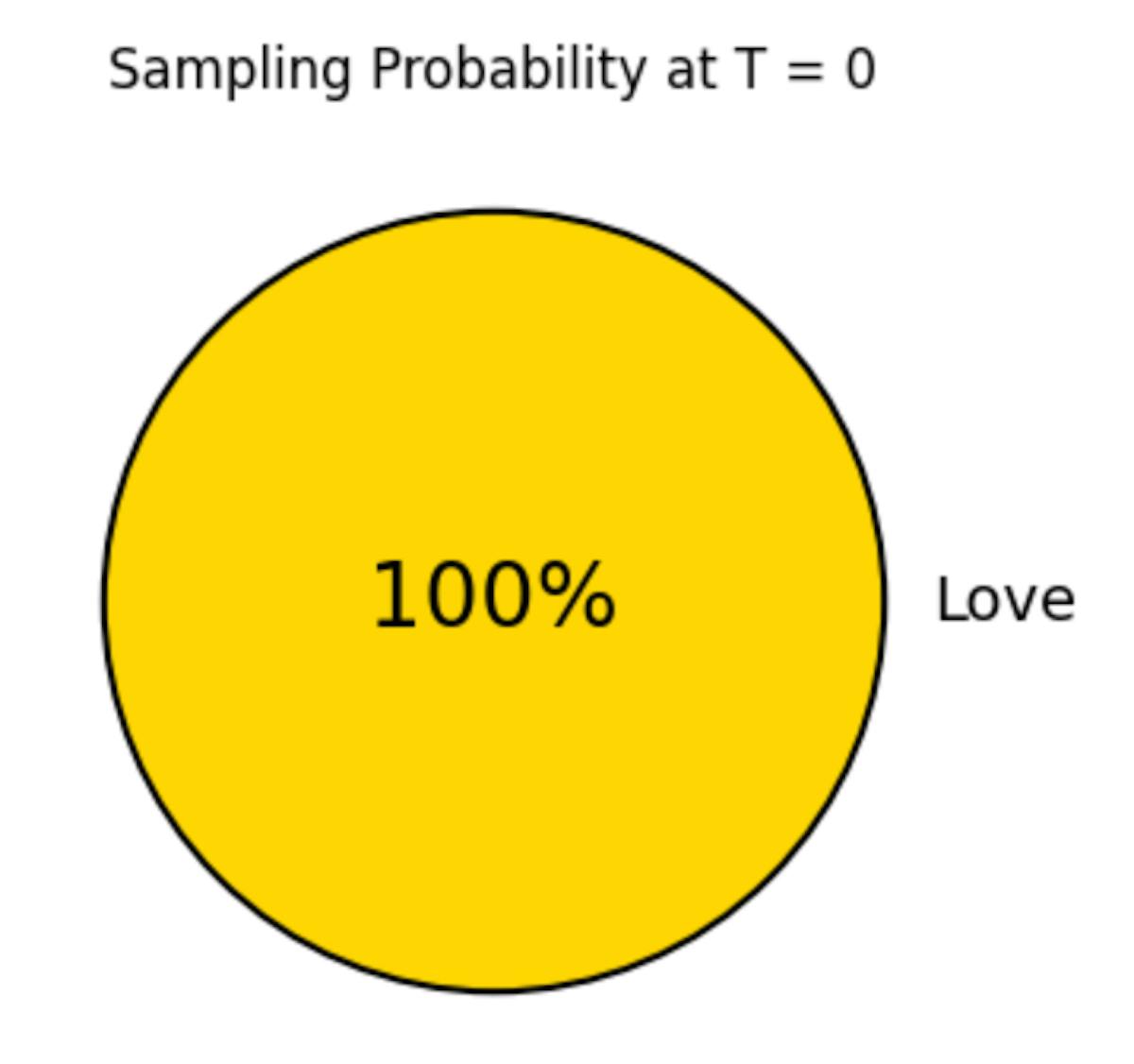
T= 0
At T = 0, we always choose the token ‘Love’
0<T<=2
- At T= 0.5, we still make the likely tokens more likely and unlikely tokens more unlikely than model probability.
- At T= 1, we recover the original model probabilities (OpenAI API default)
- At T = 2, we make the likely tokens less likely and unlikely tokens more likely than model probabilites hence the model can be more “creative” and sometimes become unhinged.
As the temperature increases, the probability distribution flattens: tokens that originally had high probabilities see those probabilities decrease, while tokens with lower probabilities see theirs increase.
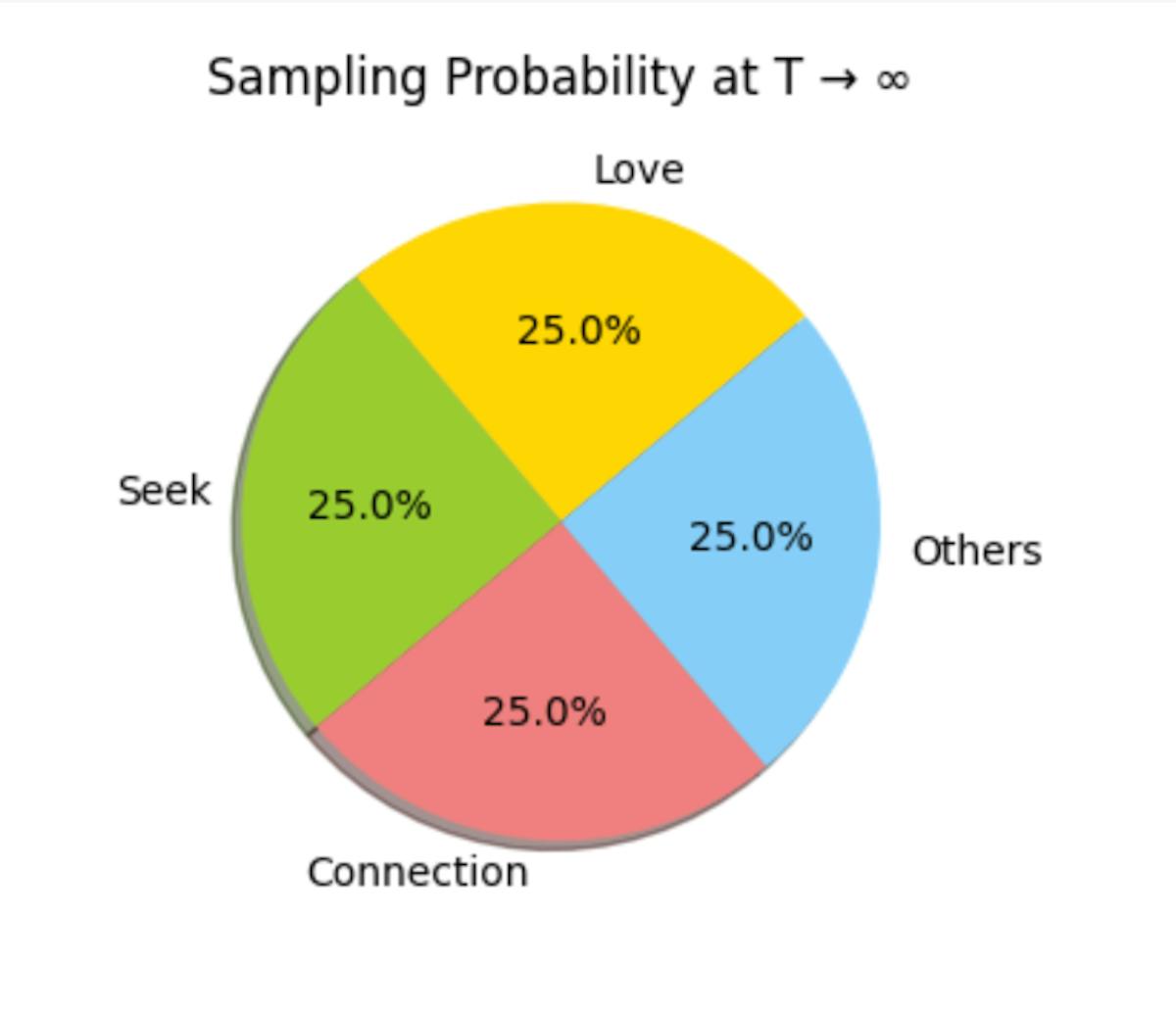
T → ♾️
As T → ♾️ we choose all tokens with equal probability (this is not allowed by the APIs and you would never do this in practice as this will produce gibberish text, here for completing our understanding of temperature)
Illustrating the effect of Temperature on Generated Text
Now let’s have some fun with the temperature settings, by taking a few samples at each temperature.
Answer with exactly two words. What is the meaning of life?
| T = 0 | T = 0.5 | T = 1.0 | T = 2.0 |
| Love others | Connection and growth | Connection and growth. | Write stories |
| Love others | Love others | Seek connection. | Beogo সবচেয়ে হচ্ছে ప్రమ vertu n conservative thème अनुप |
| Love others | Pursue happiness | Existential exploration | Compatibility waits. |
At T=0, we get the same answers all 3 times (this is theoretically expected, but may not work in practice every time – more on this later)
And we see the outputs getting more creative as the temperature increases, but also carry the risk of giving gibberish output, we get 1 gibberish output a T= 2.0 (the highest temperature value allowed in OpenAI API), where the model produces a mixture of languages. In fact, Anthropic’s Claude API limits the range of temperature from 0 to 1.
Let’s take another example with a deterministic answer.
What is 2 + 2 **3, exact numerical answer only
| T = 0 | T = 0.5 | T = 1.0 | T = 2.0 |
| 10 | 10 | 10 | 2 + 2 ** 3 = 10 |
| 10 | 10 | 10 | 10 |
| 10 | 10 | 2 + 2 ** 3 = 10 | Separator Solution darunter ക്ല 글شرات shedding Hardy(usingғым |
Here we see that for lower temperatures, we always get the correct answer. However, for T=1, we get the correct answer twice, and the third answer – though semantically correct – would break an automated system that was relying on the correct numerical answer. For T=2.0 we may still get the correct answer; however, it may also end up with gibberish.
This illustrates that lower temperatures are preferred in deterministic domains and higher temperatures in creative domains. This is the advice that you mostly read when you read documentation on temperature settings and it is correct to a first approximation. But let us dive deeper.
The special case of T = 0
So if we want deterministic answers, then we should set a temperature of 0. Does this always guarantee the same answer? In theory, yet, but in practice not. Though you do get the least variability in the answer when setting T = 0. This residual variability is because of the inference infrastructure.
Documentation for Claude: Note that even with a temperature of 0.0, the results will not be fully deterministic.
Gemini: A temperature of 0 means that the highest probability tokens are always selected. In this case, responses for a given prompt are mostly deterministic, but a small amount of variation is still possible.
OpenAI documentation does not comment specifically about T = 0 but mentions “lower values like 0.2 will make it more focused and deterministic” and “Chat Completions are non-deterministic by default”. They also provide some additional ways like setting a seed parameter and inspecting the system fingerprint for reproducible outputs.
The cons of using T = 0 boring, repetitive text, and underexplored in a chain of thought.
Using Higher Temperatures
As discussed, in longer and more creative text generation tasks, higher temperatures are preferred.
But another interesting use case is in problem-solving domains where the model may benefit from exploring multiple paths.
The paper “SELF-CONSISTENCY IMPROVES CHAIN OF THOUGHT REASONING IN LANGUAGE MODELS” makes the case for using higher temperatures. Self-consistency decoding improves chain-of-thought prompting by sampling multiple reasoning paths at higher temperatures and selecting the most consistent answer, instead of using the greedy decoding strategy (T =0). This significantly boosts performance on complex reasoning benchmarks.
Similarly, reasoning models also benefit from setting T to low values instead of 0.
Another good paper to look at is “The Effect of Sampling Temperature on Problem Solving in Large Language Models”. The charts have been reproduced directly from the paper.
Across a variety of LLMs, tasks, and prompting techniques, the accuracy remains fairly stable between temperatures of 0 and 1. They note that while accuracy on individual problems fluctuates between temperatures, the overall average accuracy across all problems stays roughly the same.
The accuracy starts dropping around T =1, and degenerates to 0 at T = 1.6.
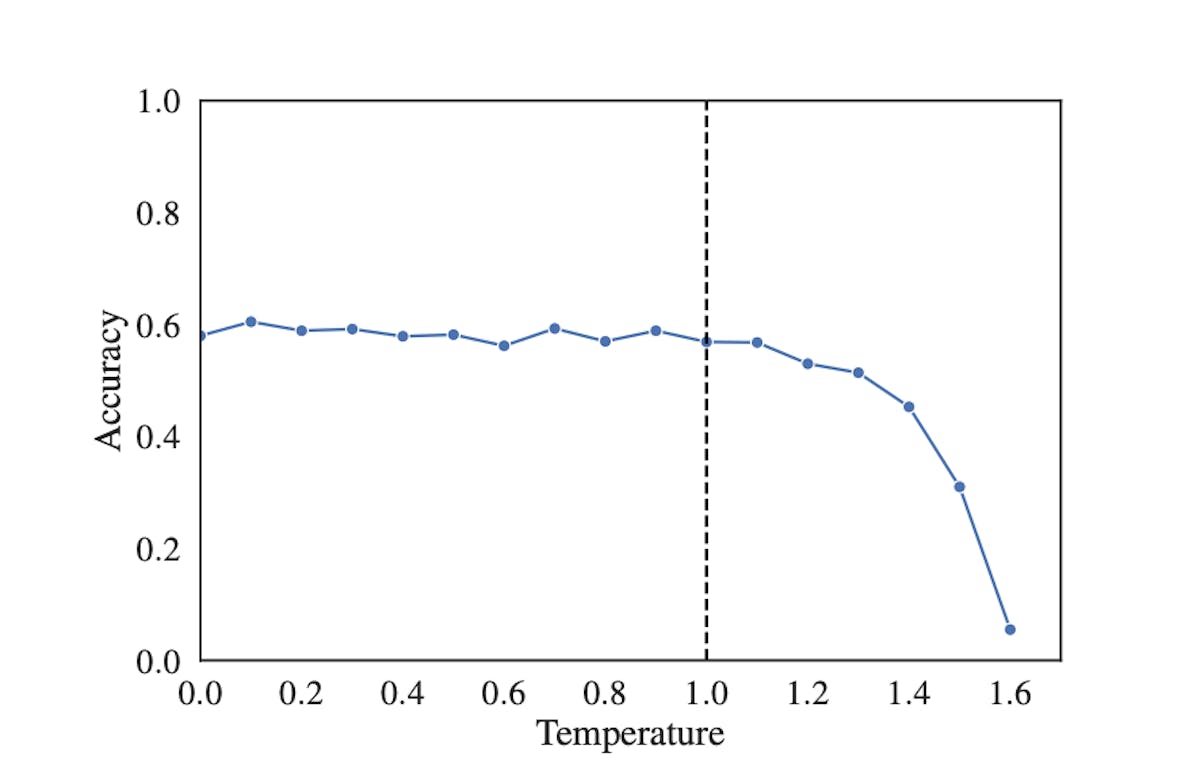
Figure reproduced from Paper
Text variability for outputs and different temperatures steadily increases from T = 0 to T=1 and falls sharply after that.
The paper recommends using T = 0 for multiple-choice/structured answer situations without worrying about performance, and exploring higher temperatures when variation in text is desirable.
This article was originally published by Misam Abbas on HackerNoon.




